一、题目
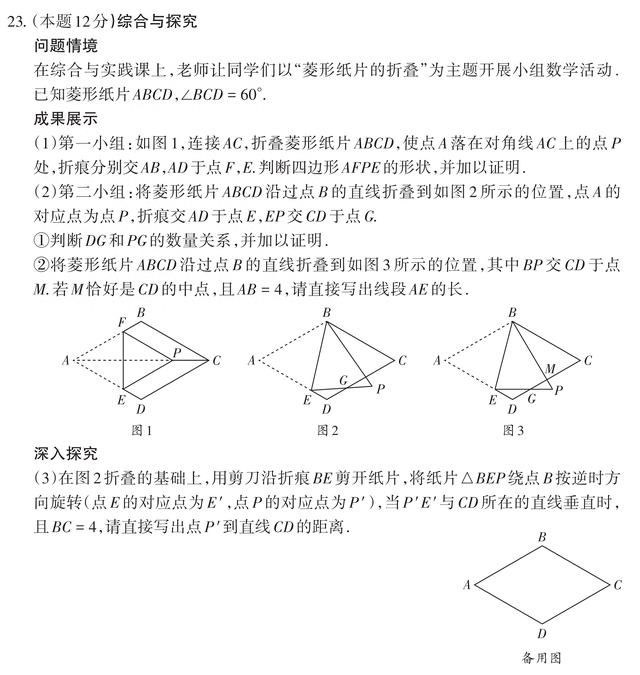
总体来讲，中规中矩，唯一不同，不是常见的三问，而是四问。
二、分析与解答
（1）考查折叠的性质和菱形的证明。
易错警示：不能由折叠得到AP垂直平分EF。
题很简单，但方法很多。
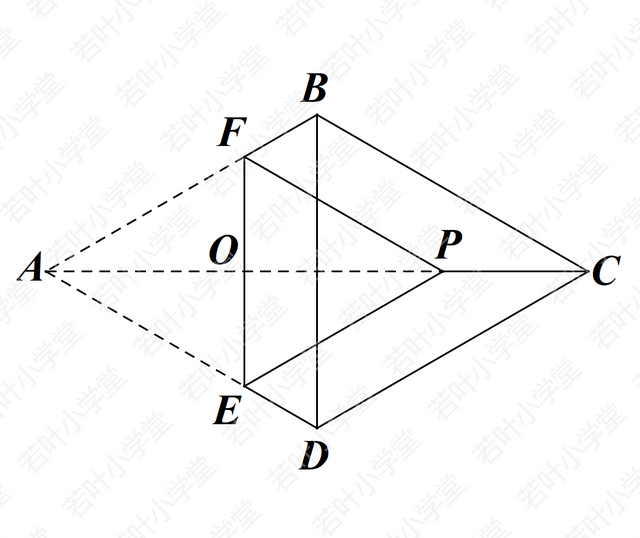
四边形AFPE为菱形，理由如下：
解法一：有一组邻边相等的平行四边形是菱形
∵四边形ABCD为菱形 ∴∠PAE=∠PAF
由折叠，知 ∠PAE=∠APE=∠PAF=∠APF
∴AF//PE，AE//PF ∴四边形AFPE为平行四边形
由折叠，知 AF=PF ∴四边形AFPE为菱形
解法二：四条边都相等的四边形是菱形
由折叠，知 AF=PF，AE=PE，∠AOE=∠AOF=90°
∵四边形ABCD为菱形 ∴∠OAE=∠OAF
又∵OA=OA ∴△AOE≌△AOF ∴AE=AF
∴AE=AF=PF=PE ∴四边形AFPE为菱形
解法三：对角线互相垂直平分的四边形是菱形
由折叠，知 ∠AOE=∠AOF=90°，OA=OP
∵四边形ABCD为菱形 ∴∠OAE=∠OAF
又∵OA=OA ∴△AOE≌△AOF ∴OE=OF
∴四边形AFPE为菱形
（2）①证边相等，可通过证全等或等腰来证明。
DG=PG，理由如下：
Ⅰ、证等腰
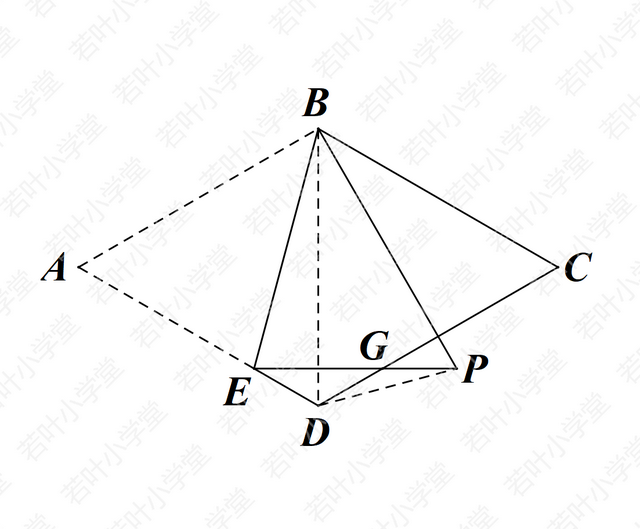
连接BD、PD
简证：易证BD=BP ∴∠BDP=∠BPD
易证∠BDC=∠BPE=60° ∴∠GDP=∠GPD ∴DG=PG
Ⅱ、证全等
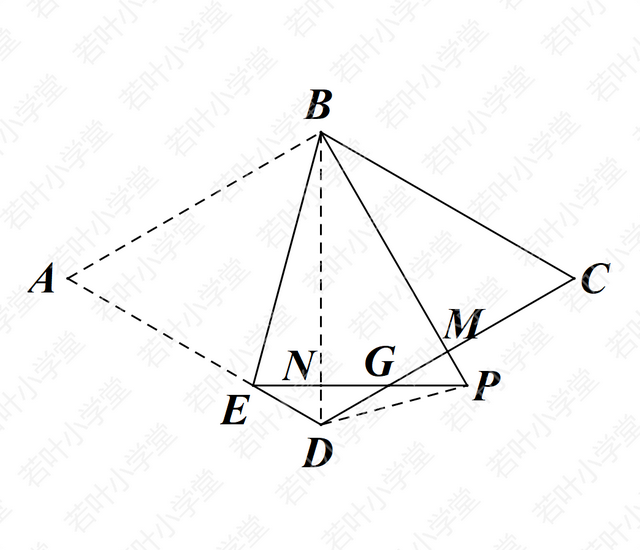
简证：易证△BDM≌△BPN(ASA) ∴BM=BN ∴PM=DN
易证△DGN≌△PGM(AAS) ∴DG=PG
②求线段长，别忘了利用①的结论
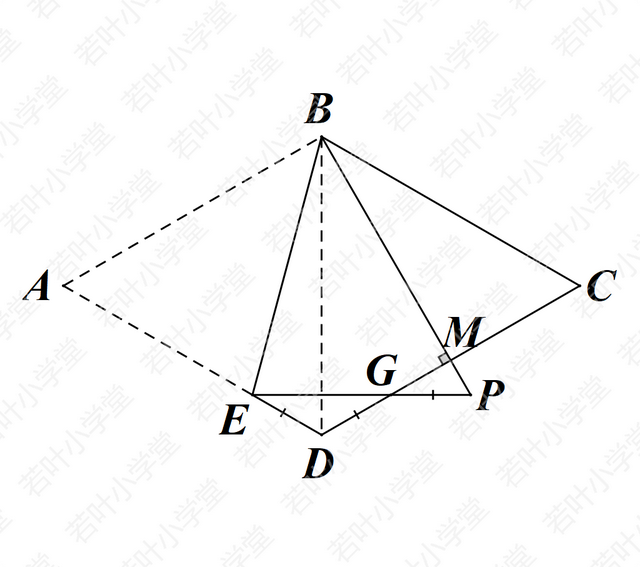
由三线合一，可得BP⊥CD
CM=1/2BC=2，BM=√3CM=2√3，PM=4-2√3
DE=DG=PG=2PM=8-4√3，AE=4-(8-4√3)=4√3-4
（3）动点问题，分类讨论，画图是关键。
图3中，PE与CD夹角为30°，顺时针转60°或逆时针转120°后，P'E'⊥CD
①顺时针旋转60°（逆时针旋转300°）
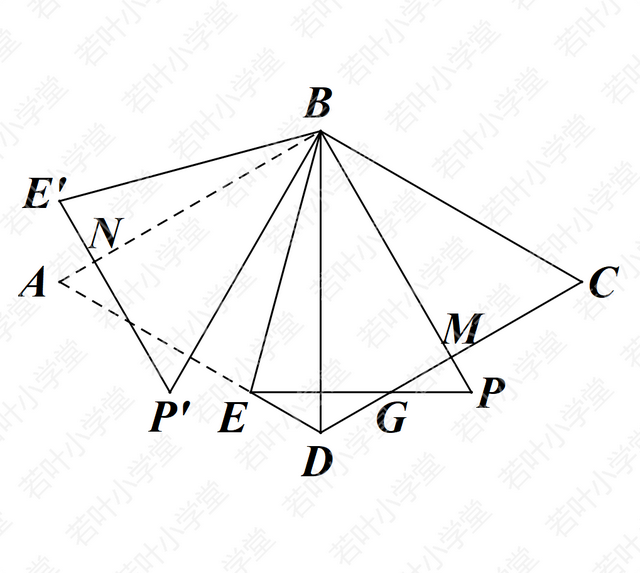
P'到CD的距离=BM-P'N=2√3-2
②逆时针旋转120°
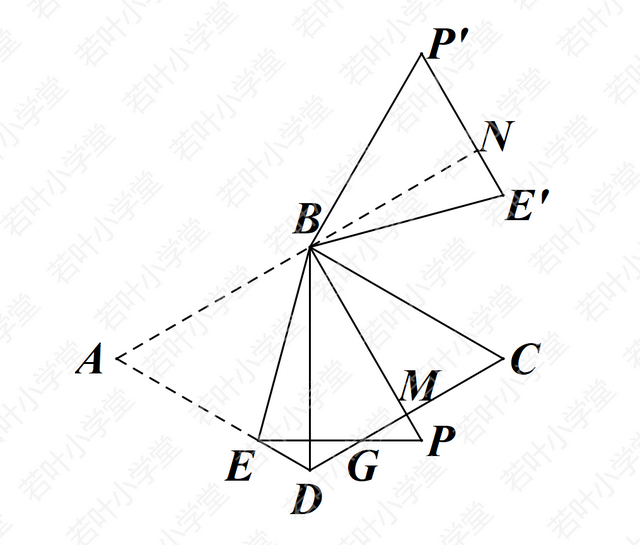
P'到CD的距离=BM+P'N=2√3+2
综上，点P'到直线CD的距离为2√3-2或2√3+2
三、小结
1、本题考查了折叠的性质、菱形的判定、证边相等、求线段长、动点画图。
2、折叠的性质：①全等；②垂直平分（折痕垂直平分对应点连线）
3、证边相等常用方法：①全等；②等腰
4、本题的求线段长只需线段的和差，重点在于理清思路，准确画出图形。
5、动点画图需要具备较强的空间想象能力和动手能力，可借助三角板或纸片旋转来理解。
互联网股票配资,杠杆炒股官网,配资平台查询官网提示：文章来自网络，不代表本站观点。
- 上一篇：炒股指杠杆平台这个晨曦愿回城特效作品
- 下一篇：没有了
